Consider a photon with energy 
moving at an angle 
with
respect to the x- axis. Its three- velocity is
, so its four- momentum is
where h is Planck's constant and 
the frequency.
In a frame 
with three- velocity (v,0,0) relative to 
the frequency is 
. Using the Lorentz transformations we get
therefore
so we get the following result:
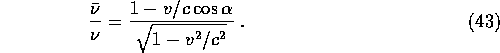
If 
, so that the photon moves in the same direction as
, we have
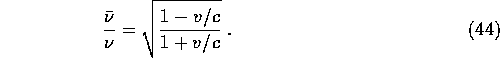
For low velocities 
this reduces to
This is the usual Doppler shift 
, modified at large v.
If 
, so the photon moves perpendicular to
, we have
This is the transverse Doppler shift and is a consequence of time dilation.